Thinking Through Dynamic Programming

What is the similarity between generating Fibonacci number and calculating the minimum editing distance of two strings?

Both of them can be solved by using dynamic programming, although 1) there is a relatively better way to generate the Fibonacci number, and 2) when we are talking about dynamic programming the implementations of the previous two questions have more differences than similarities. The former one use only two temporary variables for intermediate results, while the latter takes advantage of a 2D matrix as register to remember all results of the sub-problems.

But they do have the same train of thought if we start solving from the recursive solutions. And more importantly, this similar thought could resolve two obstacles for implementing the dynamic programming: what is the structure of the DP register (1D or 2D list), and what are the edge cases.

Take Fibonacci number as example. We have to know the number with index N-1 and N-2 so that we can derive the number of index N. The recursive solution is

fib = lambda n: fib(n-1)+fib(n-2) if n > 2 else 1

That is, for every problem, there should be two sub-problems solved before tackling it. Furthermore, the edge cases are with index 0 and 1. So, the dynamic programming version of the solution becomes:

def fib(n):
    a = 0
    b = 1
    for __ in range(n):
        a, b = b, a + b
    return a

On the other hand, the minimum distance between two strings are just “slightly” difficult. It has four cases for two given indices of the two strings: the characters are the same, so the distance is 0; one of the character needs to be deleted; one of the indices needs to insert a new character; both characters need to be replaced. The last three cases will have distance 1. Although it is a little bit obscure coming up with the 2D matrix DP solution, it is easy to write the recursive version:

def minDistance(self, word1, word2):
        def helper(pt1, pt2):
            if pt1 < 0:
                return pt2+1
            elif pt2 < 0:
                return pt1+1
            # the two characters are matched
            if word1[pt1] == word2[pt2]:
                return helper(pt1-1, pt2-1)
            else:
            # pt1 needs del, pt2 needs del, or pt1 and pt2 needs replaced
                return min(helper(pt1-1, pt2), helper(pt1, pt2-1), \
                        helper(pt1-1, pt2-1))+1
        return helper(len(word1)-1, len(word2)-1)

The local helper functions do all of the dirty work of recursively finding the minimum distance of the two substring. The termination criteria are actually the edge cases we need to construct the starting point of the dynamic programming.

If the entire first string matches the part of the second string from pointer pt2 to the end, the remaining distance is the value of pt2. The range of the pt2 is from zero to the length of the second string. As a result, it needs a 2D matrix to record all of the intermediate results, going through both the first and the second string, and the edge cases of pt1 and pt2 are analyzed above. We will have something like

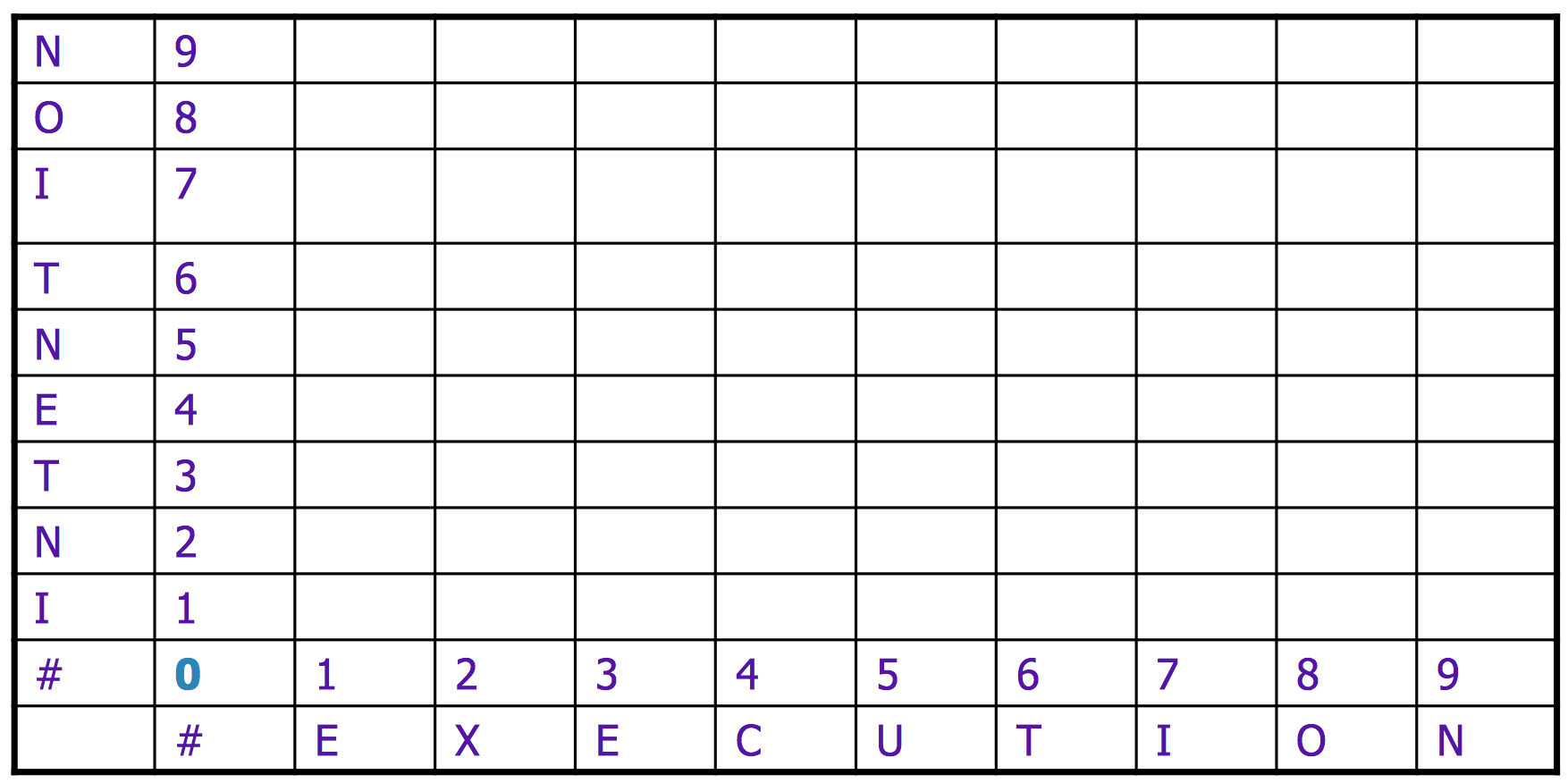
Example Table

Then, according to the recursive solution, if the two characters are different, the slot in the table is determined by three slots (plus one): its left neighbor, the slot under it, and the slot in the left under diagonal direction. If they are the same, then it is equal to the value in the left-under diagonal slot.

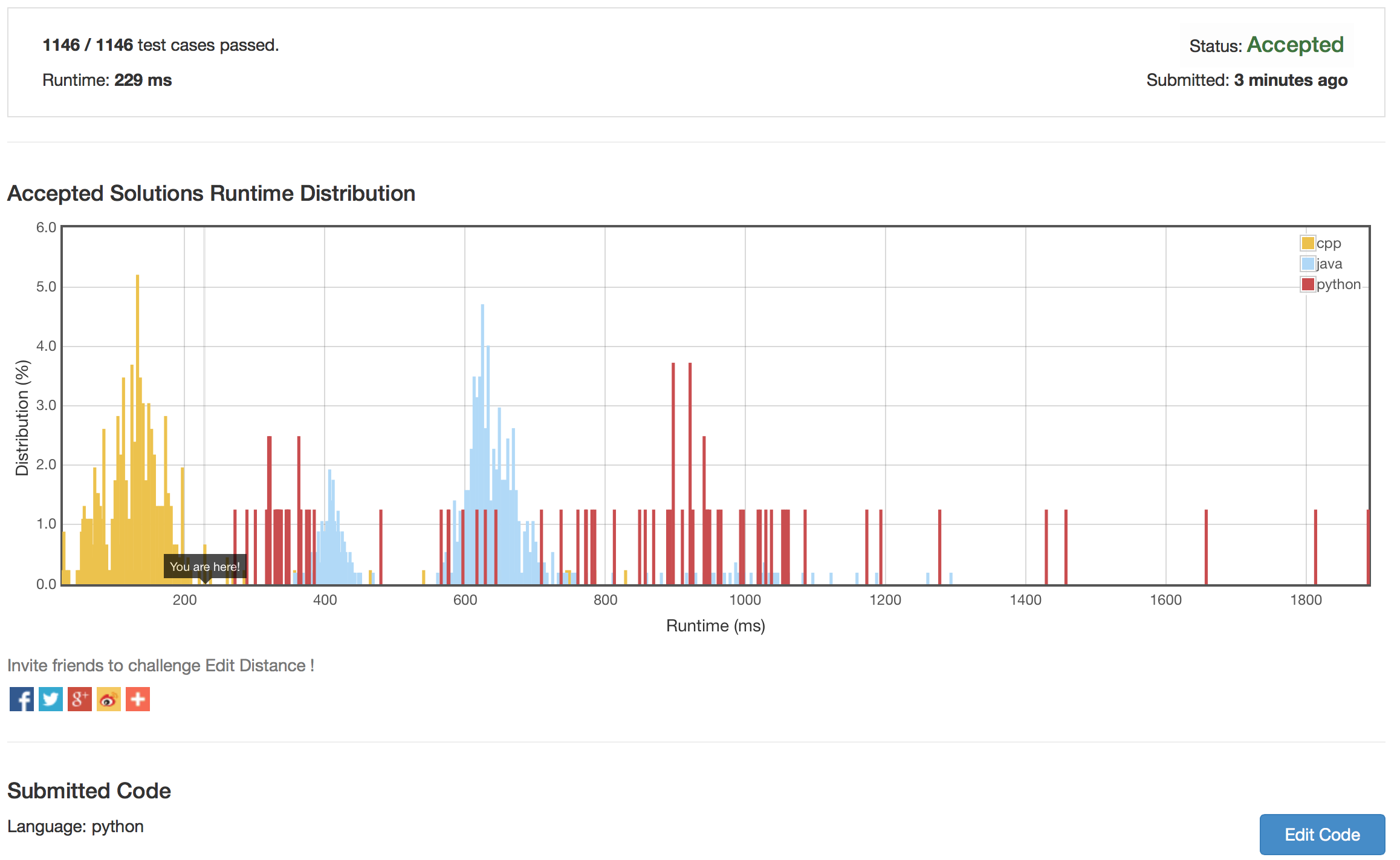
Till this step, the dp solution is complete and functioned. But further improvement can be made in the space complexity. Because each slot only needs three neighbors to make the decision, we can either go by row or go by column. Suppose the two input strings have length M and N. The final version has time complexity of O(MN) and space of O(min(M,N)).

def minDistance(self, word1, word2):
        if min(len(word1), len(word2)) == 0:
            return max(len(word1), len(word2))
        memory = range(len(word1)+1)
        for i2 in range(len(word2)):
            register = [i2+1]+[0]*len(word1)
            for i1 in range(len(word1)):
                if word1[i1] == word2[i2]:
                    register[i1+1] = memory[i1]
                else:
                    register[i1+1] = min(register[i1], memory[i1],memory[i1+1])+1
            memory = register
        return register[-1]

The optimization is quite promising. This solution achieves the best running time among python implementations.

Example Table

Reference:

Some good Q&A from Quora: